Hukum Gauss: "bahwa fluks listrik total yang melalui sembarang permukaan tertutup (sebuah permukaan yang meliputi volume tertentu) sebanding dengan muatan listrik (netto) total di dalam permukaan itu" .
Secara matematika aturan Gauss sanggup ditulis sebagai berikut.\[\small \phi =\oint \vec{E}.\vec{dA}=\frac{\sum_{i}q_{i}}{\varepsilon _{o}}\\\oint \vec{E}.\vec{dA}=\frac{q_{in}}{\varepsilon _{o}}\]Dimana $\small \oint$ ialah integral permukaan tertutup.
Penggunaan Hukum Gauss
Bila kita hendak memakai Hukum Gauss untuk memilih berpengaruh medan listrik disekitar suatu distribusi muatan kita harus memperhatikan hal-hal sebagai berikut:
Besar muatan yang dilingkupi oleh permukaan tertutup gauss M ialah Q\[\small \\\oint \vec{E}.\vec{dA}=\frac{q_{in}}{\varepsilon _{o}}\\4\pi r_{M}^{2}E=\frac{q_{in}}{\varepsilon _{o}}\]
Soal Jawab:
1. Medan listrik homogen sebesar 200 N/C ditembakkan tegak lurus ke sebuah bidang persegi dengan panjang sisi 20 cm, jumlah garis medan listrik yang menembus bidang persegi tersebut adalah....?
Jawaban Fisika Pak Dimpun :
\[\\ \Phi = E. A\cos \theta \\ \Phi = 200. 4 \times 10^{-2} \cos 0^{o} \\ \Phi = 8 \: \, Weber\]
2.Kuat medan listrik sebesar 200 N/C mengarah pada bidang bundar berjari-jari 7 cm dengan membentuk sudut 300 terhadap bidang. Tentukan berapa fluks listrik tersebut?
Jawaban Fisika Pak Dimpun :
\[\\\Phi = E. A.\cos \theta \\\Phi = E. \pi r^{2}\cos \theta \Rightarrow \theta =90-30=60^{o}\\\Phi = 200\times (3,24)(7.10^{-2}) . 0,5 \\ \Phi = 1,54 weber\]
3. Sebuah muatan titik sebesar 1,8 µC terletak di tengah-tengah sebuah kubus berjari-jari 55 cm. Hitung fluks listrik yang menembus permukaan kubus tersebut.
Jawaban Fisika Pak Dimpun :
Secara matematika aturan Gauss sanggup ditulis sebagai berikut.\[\small \phi =\oint \vec{E}.\vec{dA}=\frac{\sum_{i}q_{i}}{\varepsilon _{o}}\\\oint \vec{E}.\vec{dA}=\frac{q_{in}}{\varepsilon _{o}}\]Dimana $\small \oint$ ialah integral permukaan tertutup.Penggunaan Hukum Gauss
Bila kita hendak memakai Hukum Gauss untuk memilih berpengaruh medan listrik disekitar suatu distribusi muatan kita harus memperhatikan hal-hal sebagai berikut:
- Simetri apa yang dipunyai sistem ini, dari sini diperoleh citra kualitatif wacana medan tersebut.
- Pilih suatu permukaan (khayal) yang kita sebut permukaan Gauss yang sesuai dengan bentuk simetri diatas, melalui titik yang akan ditentukan berpengaruh medannya itu.
- Pemilihan permukaan Gauss yang sempurna akan menghasilkan E yang sama besar dan tegak lurus pada sebagian atau seluruh permukaan tertutup tersebut dan nol di permukaan lain.
Medan listrik di dalam bola 0 < r < R
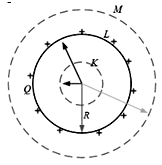
Untuk menghitung medan listrik di dalam bola berongga buatlah permukaan gauss permukaan bola K menyerupai pada gambar, kemudian gunakan aturan Gauss di bawah ini\[\small \phi =\oint \vec{E}.\vec{dA}=\frac{\sum_{i}q_{i}}{\varepsilon _{o}}\\\oint \vec{E}.\vec{dA}=\frac{q_{in}}{\varepsilon _{o}}\\\]dimana hasil $\small \oint dA=4\pi R^{2}$ sama dengan luas permukaan bola K yang dibentuk di dalam bola berongga. Nilai Q di dalam permukaan gauus yang dibentuk ialah 0 sebab tidak ada muatan yang terlingkupi di dalam permukaan gauss K.\[\small 4\pi r_{k}^{2}=\frac{0}{\varepsilon _{o}}=0\]Maka besar medan listrik di dalam bola sama dengan nolMedan listrik di permukaan bola r = R
Untuk menghitung besar medan listrik di permukaan bola, kita harus menciptakan permukaan bola gauss yang berhimpit dengan permukaan bola yaitu permukaan L, kemudian gunakan persamaan matematis aturan Gauss untuk menghitung besar medan listrik di permukaan bola.\[\small \oint \vec{E}.\vec{dA}=\frac{q_{in}}{\varepsilon _{o}}\\4\pi r_{L}^{2}E=\frac{q_{in}}{\varepsilon _{o}}\]Besar muatan yang dilingkupi oleh permukaan gauus yang berhimpit dengan permukaan bola berongga ialah Q\[\small 4\pi r_{L}^{2}E=\frac{q_{in}}{\varepsilon _{o}}\\E=\frac{q_{in}}{4\varepsilon _{o}\pi R^{2}}\Rightarrow k=\frac{1}{4\pi\varepsilon _{o}}\\\\E=k\frac{q_{in}}{R^{2}}\]Medan listrik di permukaan bola ialah \[\small E=k\frac{q_{in}}{R^{2}}\]Dengan ialah konstanta Coulomb bernilai $\small k=9.10^{9}Nm^{2}C^{-2}$Medan listrik di luar permukaan bola r > R
Untuk menghitung besar medan listrik di luar permukaan bola kita harus menciptakan permukaan gauss di luar permukaan bola berongga di gambar permukaan itu disebut permukaan M. Gunakan persamaan matematik aturan Gauss untuk menghitung besar medan listrik di luar permukaan bola berongga\[\small \\\oint \vec{E}.\vec{dA}=\frac{q_{in}}{\varepsilon _{o}}\\4\pi r_{M}^{2}E=\frac{q_{in}}{\varepsilon _{o}}\]Besar muatan yang dilingkupi oleh permukaan tertutup gauss M ialah Q\[\small \\\oint \vec{E}.\vec{dA}=\frac{q_{in}}{\varepsilon _{o}}\\4\pi r_{M}^{2}E=\frac{q_{in}}{\varepsilon _{o}}\]
1. Medan listrik homogen sebesar 200 N/C ditembakkan tegak lurus ke sebuah bidang persegi dengan panjang sisi 20 cm, jumlah garis medan listrik yang menembus bidang persegi tersebut adalah....?
Jawaban Fisika Pak Dimpun :
\[\\ \Phi = E. A\cos \theta \\ \Phi = 200. 4 \times 10^{-2} \cos 0^{o} \\ \Phi = 8 \: \, Weber\]
2.Kuat medan listrik sebesar 200 N/C mengarah pada bidang bundar berjari-jari 7 cm dengan membentuk sudut 300 terhadap bidang. Tentukan berapa fluks listrik tersebut?
Jawaban Fisika Pak Dimpun :
\[\\\Phi = E. A.\cos \theta \\\Phi = E. \pi r^{2}\cos \theta \Rightarrow \theta =90-30=60^{o}\\\Phi = 200\times (3,24)(7.10^{-2}) . 0,5 \\ \Phi = 1,54 weber\]
3. Sebuah muatan titik sebesar 1,8 µC terletak di tengah-tengah sebuah kubus berjari-jari 55 cm. Hitung fluks listrik yang menembus permukaan kubus tersebut.
Jawaban Fisika Pak Dimpun :
\[\small \\\varepsilon _{o}\oint \vec{E}.\vec{dA}=q \\\varepsilon _{o}(\Phi )=q \\\Phi=\frac{q}{\varepsilon _{o}}=\frac{1,8\times 10^{-6}}{8,85\times 10^{-12}} \\\Phi=2,034\times 20^5\: Weber\]
Post a Comment (0)